Šis raksts ir par parastās frakcijas. Šeit mēs iepazīsimies ar veseluma daļas jēdzienu, kas mūs novedīs pie parastās daļas definīcijas. Tālāk mēs pakavēsimies pie pieņemtā apzīmējuma parastajām daļām un sniegsim daļskaitļu piemērus, teiksim par daļskaitļa skaitītāju un saucēju. Pēc tam mēs sniegsim pareizo un nepareizo, pozitīvo un negatīvo daļu definīcijas, kā arī ņemsim vērā daļskaitļu atrašanās vietu koordinātu starā. Noslēgumā mēs uzskaitām galvenās darbības ar daļskaitļiem.
Lapas navigācija.
Kopuma akcijas
Vispirms mēs iepazīstinām akciju koncepcija.
Pieņemsim, ka mums ir kāds objekts, kas sastāv no vairākām absolūti identiskām (tas ir, vienādām) daļām. Skaidrības labad varat iedomāties, piemēram, ābolu, kas sagriezts vairākās vienādās daļās, vai apelsīnu, kas sastāv no vairākām vienādām šķēlītēm. Katra no šīm vienādajām daļām, kas veido visu objektu, tiek saukta daļa no kopuma vai vienkārši akcijas.
Ņemiet vērā, ka akcijas ir atšķirīgas. Paskaidrosim šo. Pieņemsim, ka mums ir divi āboli. Sagriežam pirmo ābolu divās vienādās daļās, bet otro – 6 vienādās daļās. Skaidrs, ka pirmā ābola daļa atšķirsies no otrā ābola daļas.
Atkarībā no akciju skaita, kas veido visu objektu, šīm akcijām ir savi nosaukumi. Analizēsim kopīgu vārdus. Ja objekts sastāv no divām daļām, jebkuru no tām sauc par visa objekta otro daļu; ja objekts sastāv no trim daļām, tad jebkuru no tām sauc par vienu trešo daļu utt.
Vienam sekundes sitienam ir īpašs nosaukums - puse. Viena trešdaļa tiek izsaukta trešais, un viens četrkāršs - ceturksnis.
Īsuma labad tālāk akciju apzīmējumi. Viena otrā akcija ir apzīmēta kā vai 1/2, viena trešdaļa - kā vai 1/3; viena ceturtā daļa - like vai 1/4 utt. Ņemiet vērā, ka apzīmējums ar horizontālu joslu tiek izmantots biežāk. Lai konsolidētu materiālu, sniegsim vēl vienu piemēru: ieraksts apzīmē simt sešdesmit septīto daļu no visa.
Daļas jēdziens dabiski sniedzas no objektiem līdz lielumiem. Piemēram, viens no garuma mēriem ir metrs. Lai mērītu garumus, kas mazāki par metru, var izmantot metra daļas. Tātad jūs varat izmantot, piemēram, pusmetru vai desmito vai tūkstošdaļu no metra. Līdzīgi tiek piemērotas arī citu daudzumu daļas.
Daļskaitļi, definīcijas un daļskaitļu piemēri
Lai aprakstītu akciju skaitu, tiek izmantots parastās frakcijas. Sniegsim piemēru, kas ļaus tuvoties parasto daļskaitļu definīcijai.
Ļaujiet apelsīnam sastāvēt no 12 daļām. Katra akcija šajā gadījumā ir viena divpadsmitā daļa no vesela apelsīna, tas ir, . Apzīmēsim divus sitienus kā , trīs sitienus kā un tā tālāk, 12 sitienus kā . Katru no šiem ierakstiem sauc par parasto daļskaitli.
Tagad dosim ģenerāli parasto daļskaitļu definīcija.
Parasto daļskaitļu izteiktā definīcija ļauj mums ienest parasto daļskaitļu piemēri: 5/10 , , 21/1 , 9/4 , . Un šeit ir ieraksti  neatbilst parasto daļskaitļu izteiktajai definīcijai, tas ir, tās nav parastās frakcijas.
neatbilst parasto daļskaitļu izteiktajai definīcijai, tas ir, tās nav parastās frakcijas.
Skaitītājs un saucējs
Ērtības labad mēs izšķiram parastās frakcijas skaitītājs un saucējs.
Definīcija.
Skaitītājs parastā daļa (m / n) ir naturāls skaitlis m.
Definīcija.
Saucējs parastā daļa (m / n) ir naturāls skaitlis n.
Tātad skaitītājs atrodas virs daļskaitļu joslas (pa kreisi no slīpsvītras), un saucējs atrodas zem daļskaitļu joslas (pa labi no slīpsvītras). Piemēram, ņemsim parasto daļskaitli 17/29, šīs daļdaļas skaitītājs ir skaitlis 17, bet saucējs ir skaitlis 29.
Atliek apspriest parastās daļskaitļa skaitītājā un saucējā ietverto nozīmi. Daļas saucējs parāda, no cik daļām sastāv viena vienība, skaitītājs savukārt norāda šādu daļu skaitu. Piemēram, daļskaitļa 12/5 saucējs 5 nozīmē, ka viens vienums sastāv no piecām daļām, bet skaitītājs 12 nozīmē, ka tiek ņemtas 12 šādas daļas.
Dabiskais skaitlis kā daļskaitlis ar saucēju 1
Parastās daļas saucējs var būt vienāds ar vienu. Šajā gadījumā mēs varam pieņemt, ka objekts ir nedalāms, citiem vārdiem sakot, tas ir kaut kas vesels. Šādas daļskaitļa skaitītājs norāda, cik veselu priekšmetu ir ņemts. Tādējādi formas m/1 parastajai daļai ir naturāla skaitļa m nozīme. Šādi mēs pamatojām vienādību m/1=m .
Pēdējo vienādību pārrakstīsim šādi: m=m/1 . Šī vienādība ļauj mums attēlot jebkuru naturālu skaitli m kā parastu daļskaitli. Piemēram, skaitlis 4 ir daļskaitlis 4/1, bet skaitlis 103498 ir daļa 103498/1.
Tātad, jebkuru naturālu skaitli m var attēlot kā parastu daļskaitli ar saucēju 1 kā m/1, un jebkuru parasto daļskaitli no formas m/1 var aizstāt ar naturālu skaitli m.
Daļu josla kā dalījuma zīme
Sākotnējā objekta attēlojums n daļu formā nav nekas vairāk kā sadalīšana n vienādās daļās. Pēc tam, kad prece ir sadalīta n daļās, mēs to varam sadalīt vienādi starp n cilvēkiem - katrs saņems vienu daļu.
Ja mums sākotnēji ir m identiski objekti, no kuriem katrs ir sadalīts n daļās, tad mēs varam vienādi sadalīt šos m objektus starp n cilvēkiem, piešķirot katrai personai vienu daļu no katra no m objektiem. Šajā gadījumā katrai personai būs m daļas 1/n, un m daļas 1/n dod parasto daļu m/n. Tādējādi parasto daļskaitli m/n var izmantot, lai attēlotu m vienību sadalījumu starp n cilvēkiem.
Tātad mēs ieguvām skaidru saikni starp parastajām daļām un dalīšanu (skatiet vispārējo ideju par naturālo skaitļu dalīšanu). Šīs attiecības tiek izteiktas šādi: Daļas joslu var saprast kā dalījuma zīmi, tas ir, m/n=m:n.
Ar parastās daļskaitļa palīdzību var uzrakstīt rezultātu, dalot divus naturālus skaitļus, kuriem dalīšana netiek veikta ar veselu skaitli. Piemēram, 5 ābolu dalīšanas ar 8 cilvēkiem rezultātu var uzrakstīt kā 5/8, tas ir, katrs iegūs piecas astotdaļas no ābola: 5:8=5/8.
Vienādas un nevienādas parastās daļas, daļskaitļu salīdzinājums
Diezgan dabiska darbība ir parasto daļskaitļu salīdzināšana, jo skaidrs, ka 1/12 no apelsīna atšķiras no 5/12, un 1/6 no ābola ir tāda pati kā otra 1/6 no šī ābola.
Divu parasto daļskaitļu salīdzināšanas rezultātā iegūst vienu no rezultātiem: daļas ir vai nu vienādas, vai nav vienādas. Pirmajā gadījumā mums ir vienādas kopīgās daļas, un otrajā nevienādas kopīgās daļas. Sniegsim vienādu un nevienādu parasto daļskaitļu definīciju.
Definīcija.
vienāds, ja vienādība a d=b c ir patiesa.
Definīcija.
Divas parastās frakcijas a/b un c/d nav vienāds, ja vienādība a d=b c nav izpildīta.
Šeit ir daži vienādu daļskaitļu piemēri. Piemēram, parastā daļdaļa 1/2 ir vienāda ar daļskaitli 2/4, jo 1 4=2 2 (ja nepieciešams, skatiet naturālo skaitļu reizināšanas noteikumus un piemērus). Skaidrības labad varat iedomāties divus identiskus ābolus, pirmais tiek pārgriezts uz pusēm, bet otrais - 4 daļās. Ir skaidrs, ka divas ceturtdaļas no ābola ir 1/2 daļa. Citi vienādu parasto daļskaitļu piemēri ir daļskaitļi 4/7 un 36/63, kā arī daļskaitļu pāris 81/50 un 1620/1000.
Un parastās daļskaitļi 4/13 un 5/14 nav vienādi, jo 4 14 = 56 un 13 5 = 65, tas ir, 4 14 ≠ 13 5. Vēl viens nevienlīdzīgu kopējo daļskaitļu piemērs ir daļskaitļi 17/7 un 6/4.
Ja, salīdzinot divas parastās daļskaitļus, izrādās, ka tie nav vienādi, tad, iespējams, vajadzēs noskaidrot, kura no šīm parastajām daļām mazāk cits, un kurš vairāk. Lai to noskaidrotu, tiek izmantots parasto daļskaitļu salīdzināšanas noteikums, kura būtība ir savest salīdzināmās daļskaitļus līdz kopsaucējam un pēc tam salīdzināt skaitītājus. Sīkāka informācija par šo tēmu ir apkopota rakstā daļskaitļu salīdzinājums: noteikumi, piemēri, risinājumi.
Daļskaitļi
Katra daļa ir rekords daļskaitlis. Tas ir, daļa ir tikai daļskaitļa “apvalks”, tās izskats, un visa semantiskā slodze ir precīzi ietverta daļskaitlī. Tomēr īsuma un ērtības labad daļskaitļa un daļskaitļa jēdziens tiek apvienots un vienkārši saukts par daļskaitli. Šeit der pārfrāzēt labi zināmu teicienu: sakām daļskaitli - domājam daļskaitli, sakām daļskaitli - domājam daļskaitli.
Daļas uz koordinātu stara
Visiem daļskaitļiem, kas atbilst parastajām daļskaitļiem, ir sava unikāla vieta uz , tas ir, starp daļām un koordinātu stara punktiem ir savstarpēja atbilstība.
Lai nokļūtu punktā, kas atbilst daļai m / n uz koordinātu stara, ir nepieciešams atlikt m segmentus no sākuma pozitīvā virzienā, kuru garums ir 1 / n daļa no vienības segmenta. Šādus segmentus var iegūt, sadalot vienu segmentu n vienādās daļās, ko vienmēr var izdarīt, izmantojot kompasu un lineālu.
Piemēram, uz koordinātu stara parādīsim punktu M, kas atbilst daļai 14/10. Nozares garums ar galiem punktā O un tam tuvākajā punktā, kas atzīmēts ar nelielu domuzīmi, ir 1/10 no vienības segmenta. Punkts ar koordinātu 14/10 tiek noņemts no sākuma ar 14 šādiem segmentiem.

Vienādas daļas atbilst vienam un tam pašam daļskaitlim, tas ir, vienādas daļas ir viena un tā paša punkta koordinātas uz koordinātu stara. Piemēram, viens punkts atbilst koordinātām 1/2, 2/4, 16/32, 55/110 uz koordinātu stara, jo visas rakstītās daļas ir vienādas (tas atrodas attālumā no vienības segmenta puses, atlikts no plkst. izcelsme pozitīvā virzienā).
Horizontālā un pa labi vērstā koordinātu starā punkts, kura koordināte ir liela daļa, atrodas pa labi no punkta, kura koordināte ir mazāka daļa. Tāpat punkts ar mazāko koordinātu atrodas pa kreisi no punkta ar lielāko koordinātu.
Pareizās un nepareizās daļskaitļi, definīcijas, piemēri
Starp parastajām frakcijām ir pareizās un nepareizās frakcijas. Šajā iedalījumā pamatā ir skaitītāja un saucēja salīdzinājums.
Sniegsim pareizu un nepareizo parasto daļskaitļu definīciju.
Definīcija.
Pareiza frakcija ir parasta daļa, kuras skaitītājs ir mazāks par saucēju, tas ir, ja m Definīcija.
Nepareiza frakcija ir parasta daļa, kurā skaitītājs ir lielāks vai vienāds ar saucēju, tas ir, ja m≥n, tad parastā daļa ir nepareiza. Šeit ir daži pareizu daļskaitļu piemēri: 1/4 , , 32 765/909 003 . Patiešām, katrā no uzrakstītajām parastajām daļām skaitītājs ir mazāks par saucēju (ja nepieciešams, skatiet rakstu naturālo skaitļu salīdzinājumu), tāpēc tie ir pareizi pēc definīcijas. Un šeit ir nepareizo daļskaitļu piemēri: 9/9, 23/4,. Patiešām, pirmās rakstītās parastās daļas skaitītājs ir vienāds ar saucēju, un atlikušajās daļās skaitītājs ir lielāks par saucēju. Ir arī pareizas un nepareizas daļskaitļu definīcijas, kuru pamatā ir daļskaitļu salīdzināšana ar vienu. Definīcija. pareizi ja tas ir mazāks par vienu. Definīcija. Parasto daļu sauc nepareizi, ja tas ir vienāds ar vienu vai lielāks par 1 . Tātad parastā daļa 7/11 ir pareiza, jo 7/11<1
, а обыкновенные дроби 14/3
и 27/27
– неправильные, так как 14/3>1 un 27/27 = 1 . Padomāsim par to, kā parastās daļskaitļi, kuru skaitītājs ir lielāks vai vienāds ar saucēju, ir pelnījuši šādu nosaukumu - "nepareizi". Kā piemēru ņemsim nepareizo daļskaitli 9/9. Šī daļa nozīmē, ka tiek ņemtas deviņas objekta daļas, kas sastāv no deviņām daļām. Tas ir, no pieejamajām deviņām akcijām mēs varam izveidot veselu tēmu. Tas ir, nepareizā daļa 9/9 būtībā dod veselu objektu, tas ir, 9/9 = 1. Parasti nepareizas daļskaitļi ar skaitītāju, kas vienāds ar saucēju, apzīmē vienu veselu objektu, un šādu daļu var aizstāt ar naturālu skaitli 1. Tagad apsveriet nepareizās frakcijas 7/3 un 12/4. Ir pilnīgi skaidrs, ka no šīm septiņām trešdaļām mēs varam izveidot divus veselus objektus (viens vesels objekts ir 3 daļas, tad, lai sastādītu divus veselus objektus, mums vajag 3 + 3 = 6 daļas) un viena trešā daļa joprojām būs. Tas ir, nepareizā daļa 7/3 būtībā nozīmē 2 vienības un pat 1/3 no šādas vienības daļas. Un no divpadsmit ceturkšņiem mēs varam izgatavot trīs veselus objektus (trīs objektus ar četrām daļām katrā). Tas ir, daļa 12/4 būtībā nozīmē 3 veselus objektus. Aplūkotie piemēri liek izdarīt šādu secinājumu: nepareizās daļskaitļus var aizstāt vai nu ar naturāliem skaitļiem, kad skaitītājs tiek dalīts ar saucēju (piemēram, 9/9=1 un 12/4=3), vai ar naturālu skaitli un pareizu daļskaitli, ja skaitītājs nedalās vienmērīgi ar saucēju (piemēram, 7/3=2+1/3 ). Varbūt tieši tas ir tas, ko nepareizās frakcijas ir pelnījušas šādu nosaukumu - “nepareizi”. Īpaši interesanti ir nepareizas daļskaitļa attēlojums kā naturāla skaitļa un pareizas daļskaitļa summa (7/3=2+1/3). Šo procesu sauc par veselas skaitļa daļas izņemšanu no nepareizas daļskaitļa, un tas ir pelnījis atsevišķu un rūpīgāku apsvērumu. Ir arī vērts atzīmēt, ka pastāv ļoti cieša saistība starp nepareizām daļskaitļiem un jauktiem skaitļiem. Katra parasta daļa atbilst pozitīvam daļskaitlim (skat. rakstu pozitīvie un negatīvie skaitļi). Tas ir, parastās frakcijas ir pozitīvas frakcijas. Piemēram, parastās daļskaitļi 1/5, 56/18, 35/144 ir pozitīvas daļas. Kad nepieciešams uzsvērt daļskaitļa pozitivitāti, tad tai priekšā liek plusa zīmi, piemēram, +3/4, +72/34. Ja parastas daļskaitļa priekšā ievietojat mīnusa zīmi, tad šis ieraksts atbildīs negatīvam daļskaitļam. Šajā gadījumā var runāt par negatīvās daļas. Šeit ir daži negatīvo daļskaitļu piemēri: −6/10 , −65/13 , −1/18 . Pozitīvās un negatīvās daļas m/n un −m/n ir pretēji skaitļi. Piemēram, daļskaitļi 5/7 un −5/7 ir pretējas daļas. Pozitīvas daļas, tāpat kā pozitīvi skaitļi kopumā, apzīmē pieaugumu, ienākumus, kādas vērtības izmaiņas uz augšu utt. Negatīvās daļas atbilst izdevumiem, parādiem, jebkuras vērtības izmaiņām samazinājuma virzienā. Piemēram, negatīvu daļu -3/4 var interpretēt kā parādu, kura vērtība ir 3/4. Uz horizontālās un pa labi vērstās negatīvās daļas atrodas pa kreisi no atskaites punkta. Koordinātu taisnes punkti, kuru koordinātes ir pozitīvā daļa m/n un negatīvā daļa −m/n, atrodas vienādā attālumā no sākuma, bet punkta O pretējās pusēs. Šeit ir vērts pieminēt formas 0/n daļas. Šīs daļas ir vienādas ar skaitli nulle, tas ir, 0/n=0 . Pozitīvās frakcijas, negatīvās daļas un 0/n daļas apvienojas, veidojot racionālus skaitļus. Vienu darbību ar parastajām daļskaitļiem - daļskaitļu salīdzināšanu - mēs jau aplūkojām iepriekš. Ir definētas vēl četras aritmētikas darbības ar daļskaitļiem- daļu saskaitīšana, atņemšana, reizināšana un dalīšana. Pakavēsimies pie katra no tiem. Darbību ar daļskaitļiem vispārējā būtība ir līdzīga atbilstošo darbību ar naturāliem skaitļiem būtībai. Zīmēsim analoģiju. Daļskaitļu reizināšana var uzskatīt par darbību, kurā no daļskaitļa tiek atrasta daļa. Lai precizētu, ņemsim piemēru. Pieņemsim, ka mums ir 1/6 no ābola un mums ir jāņem 2/3 no tā. Mums vajadzīgā daļa ir daļskaitļu 1/6 un 2/3 reizināšanas rezultāts. Divu parasto daļskaitļu reizināšanas rezultāts ir parasta daļa (kas konkrētā gadījumā ir vienāda ar naturālu skaitli). Tālāk mēs iesakām izpētīt rakstu daļu reizināšanas informāciju - noteikumus, piemērus un risinājumus. Bibliogrāfija. Vienosimies, ka "darbības ar daļskaitļiem" mūsu nodarbībā tiks saprastas kā darbības ar parastām daļām. Daļa ir daļa, kurai ir tādi atribūti kā skaitītājs, daļskaitļu josla un saucējs. Tas atšķir parasto daļskaitli no decimāldaļskaitļa, ko iegūst no parastās, saucēju reducējot līdz 10. Decimāldaļdaļa tiek rakstīta ar komatu, kas atdala veselo skaitļu daļu no daļskaitļa. Mēs runāsim par operācijām ar parastajām daļskaitļiem, jo tieši tās rada vislielākās grūtības skolēniem, kuri ir aizmirsuši šīs tēmas pamatus, kas apskatīti skolas matemātikas kursa pirmajā pusē. Tajā pašā laikā, pārveidojot izteiksmes augstākajā matemātikā, galvenokārt tiek izmantotas darbības ar parastajiem daļskaitļiem. Daži daļskaitļu saīsinājumi ir ko vērti! Decimāldaļskaitļi nesagādā īpašas grūtības. Tātad uz priekšu! Divas daļas un sauc par vienādām, ja . Piemēram, tāpēc Daļskaitļi un (kopš ), un (kopš ) arī ir vienādi. Acīmredzot abas daļas un ir vienādas. Tas nozīmē, ka, ja dotās daļas skaitītāju un saucēju reizina vai dala ar vienu un to pašu naturālo skaitli, tad tiks iegūta daļa, kas vienāda ar doto:. Šo īpašību sauc par frakcijas pamatīpašību. Daļas pamatīpašību var izmantot, lai mainītu daļskaitļa skaitītāja un saucēja zīmes. Ja daļskaitļa skaitītāju un saucēju reizina ar -1, tad iegūstam. Tas nozīmē, ka daļskaitļa vērtība nemainīsies, ja vienlaikus tiek mainītas skaitītāja un saucēja zīmes. Ja maināt zīmi tikai skaitītājam vai tikai saucējam, tad daļskaitlis mainīs savu zīmi: Izmantojot daļskaitļa pamatīpašību, jūs varat aizstāt doto daļskaitli ar citu daļu, kas ir vienāda ar doto daļu, bet ar mazāku skaitītāju un saucēju. Šo aizstāšanu sauc par frakciju samazināšanu. Piemēram, tiek dota daļa. Skaitļiem 36 un 48 ir lielākais kopīgais dalītājs 12. Tad Vispārīgā gadījumā daļskaitļu samazināšana vienmēr ir iespējama, ja skaitītājs un saucējs nav pirmskaitļi. Ja skaitītājs un saucējs ir nosacīti pirmskaitļi, tad daļu sauc par nereducējamu. Tātad daļskaitļa samazināšana nozīmē dalītājas skaitītāju un saucēju ar kopīgu koeficientu. Viss iepriekš minētais attiecas uz frakcionētām izteiksmēm, kas satur mainīgos. 1. piemērs Samazināt frakciju Risinājums. Lai skaitītāju sadalītu faktoros, iepriekš uzrādot monomu - 5 xy kā summa - 2 xy - 3xy, saņemam Lai faktorizētu saucēju, mēs izmantojam kvadrātu starpības formulu: Rezultātā Ļaujiet divām daļām un ir dota. Tiem ir dažādi saucēji: 5 un 7. Izmantojot daļskaitļa pamatīpašību, jūs varat aizstāt šīs daļdaļas ar tām līdzvērtīgām daļām un tādām, lai iegūtajām daļām būtu vienādi saucēji. Reizinot skaitītāju un saucēju ar 7, mēs iegūstam Reizinot skaitītāju un saucēju ar 5, mēs iegūstam Tātad daļskaitļi tiek samazināti līdz kopsaucējam: Bet tas nav vienīgais problēmas risinājums: piemēram, šīs frakcijas var arī samazināt līdz kopsaucējam 70: un vispār uz jebkuru saucēju, kas dalās gan ar 5, gan ar 7. Apskatīsim vēl vienu piemēru: samazinām daļu un līdz kopsaucējam. Argumentējot tāpat kā iepriekšējā piemērā, mēs iegūstam Bet šajā gadījumā jūs varat apvienot daļskaitļus līdz kopsaucējam, kas ir mazāks par šo daļu saucēju reizinājumu. Atrodiet 24 un 30 mazāko kopīgo daudzkārtni: LCM(24, 30) = 120 . Tā kā 120:4=5, lai uzrakstītu daļskaitli ar saucēju 120, gan skaitītājs, gan saucējs jāreizina ar 5, šo skaitli sauc par papildu koeficientu. Līdzekļi Tālāk mēs iegūstam 120:30=4. Daļas skaitītāju un saucēju reizinot ar papildu koeficientu 4, mēs iegūstam Tātad šīs daļas tiek reducētas līdz kopsaucējam. Šo daļu saucēju mazākais kopsaucējs ir mazākais iespējamais kopsaucējs. Daļskaitļu izteiksmēm, kurās ir iekļauti mainīgie, kopsaucējs ir polinoms, kas dalās ar katras daļas saucēju. 2. piemērs Atrodiet daļskaitļu kopsaucēju un . Risinājums. Šo daļu kopsaucējs ir polinoms, jo tas dalās gan ar, gan ar. Tomēr šis polinoms nav vienīgais, kas var būt šo daļu kopsaucējs. Tas var būt arī polinoms Mūsu piemērā mazākais kopsaucējs ir . Ieguva: Mums izdevās novest daļskaitļus līdz mazākajam kopsaucējam. Tas notika, pirmās daļas skaitītāju un saucēju reizinot ar , bet otrās daļdaļas skaitītāju un saucēju - ar . Polinomus un sauc par papildu faktoriem attiecīgi pirmajai un otrajai frakcijai. Frakciju pievienošana ir definēta šādi: Piemēram, Ja b = d, Tas Tas nozīmē, ka, lai pievienotu daļskaitļus ar vienu un to pašu saucēju, pietiek pievienot skaitītājus un atstāt saucēju to pašu. Piemēram, Ja saskaita daļskaitļus ar dažādiem saucējiem, tad daļskaitļus parasti samazina līdz mazākajam kopsaucējam un pēc tam pievieno skaitītājus. Piemēram, Tagad apsveriet piemēru, kā pievienot daļveida izteiksmes ar mainīgajiem. 3. piemērs Pārvērst izteiksmi par vienu daļu Risinājums. Atradīsim mazāko kopsaucēju. Lai to izdarītu, mēs vispirms faktorizējam saucējus. Frakcija- skaitļa attēlojuma forma matemātikā. Slīpsvītra norāda dalīšanas darbību. skaitītājs frakcijas sauc par dividendēm un saucējs- dalītājs. Piemēram, daļskaitlī skaitītājs ir 5 un saucējs ir 7. pareizi Daļskaitli sauc, ja skaitītāja modulis ir lielāks par saucēja moduli. Ja daļa ir pareiza, tad tās vērtības modulis vienmēr ir mazāks par 1. Visas pārējās daļas ir nepareizi. Tiek saukta frakcija sajaukts ja tas ir uzrakstīts kā vesels skaitlis un daļa. Tas ir tāds pats kā šī skaitļa un daļskaitļa summa: Ja daļskaitļa skaitītāju un saucēju reizina ar vienu un to pašu skaitli, tad daļdaļas vērtība nemainīsies, tas ir, piemēram, Lai divas daļdaļas apvienotu līdz kopsaucējam, jums ir nepieciešams: Papildinājums. Lai pievienotu divas frakcijas, jums ir nepieciešams Piemērs: Atņemšana. Lai atņemtu vienu daļu no citas, Piemērs: Reizināšana. Lai reizinātu vienu daļu ar citu, reiziniet to skaitītājus un saucējus: Divīzija. Lai dalītu vienu daļu ar citu, pirmās daļas skaitītāju reiziniet ar otrās daļas saucēju un pirmās daļas saucēju ar otrās daļas skaitītāju: Frakciju paplašināšana. Frakciju samazināšana. Frakciju salīdzinājums.
Samazinājums līdz kopsaucējam. Saskaitīšana un atņemšana
frakcijas. Daļskaitļu reizināšana. Frakciju dalīšana .
Frakciju paplašināšana.
Daļas vērtība nemainās, ja tās skaitītāju un saucēju reizina ar vienu un to pašu skaitli, kas nav nulle.
frakcijas paplašināšana. Piemēram, Frakciju samazināšana.
Daļas vērtība nemainās, dalot tās skaitītāju.
un saucēju uz to pašu skaitli, kas nav nulle
. Šo transformāciju sauc frakcijas samazināšana. Piemēram,
Frakciju salīdzinājums.
No divām daļām ar vienādu skaitītāju lielākā ir tā, kuras saucējs ir mazāks: No divām daļām ar vienādiem saucējiem tā, kurai ir lielāks skaitītājs, ir lielāka: Lai salīdzinātu daļskaitļus, kuriem ir dažādi skaitītāji un saucēji, tie ir jāpaplašina, lai apvienotu tos līdz kopsaucējam. PIEMĒRS Salīdziniet divas frakcijas: Izmantots šeit transformācija sauca reducējot daļskaitļus līdz kopsaucējam.
Daļskaitļu saskaitīšana un atņemšana.
Ja daļskaitļu saucēji ir vienādi, tad, lai saskaitītu daļskaitļus, ir jāsaskaita to skaitītāji, un, lai atņemtu daļskaitļus, ir jāatņem to skaitītāji (tādā pašā secībā). Iegūtā summa vai starpība būs rezultāta skaitītājs; saucējs paliks nemainīgs. Ja daļskaitļu saucēji ir atšķirīgi, vispirms jāsamazina daļas līdz kopsaucējam. Saskaitot jauktos skaitļus, to veselās un daļskaitļu daļas tiek pievienotas atsevišķi. Atņemot jauktos skaitļus, ieteicams vispirms tos pārvērst nepareizo daļskaitļu formā, pēc tam atņemt vienu no otra un pēc tam vēlreiz samaziniet rezultātu, ja nepieciešams, līdz jaukta skaitļa formai. PIEMĒRS
Daļskaitļu reizināšana.
Skaitli reizināt ar daļskaitli nozīmē reizināt ar skaitītāju un reizinājumu dalīt ar saucēju. Tāpēc mums ir vispārīgs noteikums daļskaitļu reizināšanai: lai reizinātu daļskaitļus, to skaitītāji un saucēji jāreizina atsevišķi un pirmais reizinājums jāsadala ar otro.
Šajā sadaļā aplūkotas darbības ar parastajām daļskaitļiem. Ja nepieciešams veikt matemātisku darbību ar jauktiem skaitļiem, tad pietiek pārveidot jaukto daļskaitli ārkārtējā, veikt nepieciešamās darbības un, ja nepieciešams, gala rezultātu vēlreiz uzrādīt kā jauktu skaitli. Šī darbība tiks aprakstīta tālāk. matemātiskā darbība. Frakciju samazināšana Lai samazinātu daļu \frac(m)(n), jāatrod lielākais tās skaitītāja un saucēja kopējais dalītājs: gcd(m,n), pēc tam dala skaitītāju un saucēju ar šo skaitli. Ja gcd(m,n)=1, tad daļu nevar samazināt. Piemērs: \frac(20)(80)=\frac(20:20)(80:20)=\frac(1)(4) Parasti uzreiz atrast lielāko kopīgo dalītāju ir sarežģīts uzdevums, un praksē daļa tiek samazināta vairākos posmos, soli pa solim izceļot acīmredzamus kopīgos faktorus no skaitītāja un saucēja. \frac(140)(315)=\frac(28\cdot5)(63\cdot5)=\frac(4\cdot7\cdot5)(9\cdot7\cdot5)=\frac(4)(9) matemātiskā darbība. Daļskaitļu apvienošana kopsaucējā Lai divas daļas \frac(a)(b) un \frac(c)(d) samazinātu līdz kopsaucējam, jums ir nepieciešams: Tādējādi mēs pārvēršam sākotnējās daļas par daļām ar vienādiem saucējiem (kas būs vienādi ar skaitli M). Piemēram, daļskaitļiem \frac(5)(6) un \frac(4) (9) ir LCM(6,9) = 18. Tad: \frac(5)(6)=\frac(5\cdot3) (6 \cdot3)=\frac(15)(18);\quad\frac(4)(9)=\frac(4\cdot2)(9\cdot2)=\frac(8)(18) . Tādējādi iegūtajām daļām ir kopsaucējs. Praksē saucēju mazākā daudzkārtņa (LCM) atrašana ne vienmēr ir viegls uzdevums. Tāpēc par kopsaucēju tiek izvēlēts skaitlis, kas vienāds ar sākotnējo daļskaitļu saucēju reizinājumu. Piemēram, daļskaitļi \frac(5)(6) un \frac(4)(9) tiek reducēti līdz kopsaucējam N=6\cdot9: \frac(5)(6)=\frac(5\cdot9)(6\cdot9)=\frac(45)(54);\quad\frac(4)(9)=\frac(4\cdot6)( 9\cdot6)=\frac(24)(54) matemātiskā darbība. Frakciju salīdzinājums Lai salīdzinātu divas parastās frakcijas: Salīdzinot frakcijas, ir vairāki īpaši gadījumi: Uzmanību! 1. noteikums attiecas uz visām daļskaitļiem, ja to kopsaucējs ir pozitīvs skaitlis. 2. un 3. noteikums attiecas uz pozitīvajām daļām (kurām gan skaitītājs, gan saucējs ir lielāks par nulli). matemātiskā darbība. Daļskaitļu saskaitīšana un atņemšana Lai pievienotu divas frakcijas, jums ir nepieciešams: Piemērs: \frac(7)(9)+\frac(4)(7)=\frac(7\cdot7)(9\cdot7)+\frac(4\cdot9)(7\cdot9)=\frac(49) )(63)+\frac(36)(63)=\frac(49+36)(63)=\frac(85)(63) Lai no vienas atņemtu vēl vienu daļu, jums ir nepieciešams: Piemērs: \frac(4)(15)-\frac(3)(5)=\frac(4)(15)-\frac(3\cdot3)(5\cdot3)=\frac(4)(15) -\frac(9)(15)=\frac(4-9)(15)=\frac(-5)(15)=-\frac(5)(3\cdot5)=-\frac(1)( 3) Ja sākotnējām daļām sākotnēji ir kopsaucējs, tad 1. punkts (samazināšana līdz kopsaucējam) tiek izlaists. matemātiskā darbība. Jaukta skaitļa pārvēršana nepareizā daļskaitlī un otrādi Lai pārvērstu jauktu frakciju par nepareizu, pietiek ar to, lai visu jauktās frakcijas daļu summētu ar frakcionēto daļu. Šādas summas rezultāts būs nepareiza daļdaļa, kuras skaitītājs ir vienāds ar veselās skaitļa daļas reizinājuma summu un daļdaļas saucēju ar jauktās daļas skaitītāju, un saucējs paliek nemainīgs. Piemēram, 2\frac(6)(11)=2+\frac(6)(11)=\frac(2\cdot11)(11)+\frac(6)(11)=\frac(2\cdot11+ 6)(11)=\frac(28)(11) Lai nepareizu daļskaitli pārvērstu par jauktu skaitli: Piemēram, daļa \frac(23)(4) . Dalot 23:4=5,75, tas ir, veselā skaitļa daļa ir 5, dalījuma atlikusī daļa ir 23-5*4=3. Tad jauktais skaitlis tiks uzrakstīts: 5\frac(3)(4) . \frac(23)(4)=\frac(5\cdot4+3)(4)=5\frac(3)(4) matemātiskā darbība. Decimāldaļas pārvēršana parastā daļskaitlī Lai decimāldaļu pārvērstu par parastu daļskaitli: 1. piemērs: 0,0089=\frac(89)(10000) (4 zīmes aiz komata, tātad saucējs 10 4 =10000, jo veselā skaitļa daļa ir 0, skaitītājs ir skaitlis aiz komata bez nullēm sākumā) 2. piemērs: 31.0109=\frac(310109)(10000) (skaitītājā ierakstām skaitli aiz komata ar visām nullēm: "0109", un tad pirms tā pievienojam sākotnējā skaitļa "31" veselo daļu) Ja decimāldaļskaitļa veselā daļa atšķiras no nulles, tad to var pārvērst par jauktu daļu. Lai to izdarītu, mēs pārvēršam skaitli parastā daļskaitlī tā, it kā veselā skaitļa daļa būtu vienāda ar nulli (punkts 1 un 2), un vienkārši pārrakstiet veselo skaitļa daļu pirms daļdaļas - tā būs jauktā skaitļa veselā daļa. Piemērs: 3,014=3\frac(14)(100) Lai parasto daļskaitli pārvērstu decimāldaļā, pietiek ar to, lai skaitītāju vienkārši sadalītu ar saucēju. Dažreiz jūs saņemat bezgalīgu decimāldaļu. Šajā gadījumā ir nepieciešams noapaļot līdz vajadzīgajai zīmei aiz komata. Piemēri: \frac(401)(5)=80.2;\quad \frac(2)(3)\apmēram 0,6667 matemātiskā darbība. Daļskaitļu reizināšana un dalīšana Lai reizinātu divas parastās daļskaitļus, jums jāreizina daļu skaitītāji un saucēji. \frac(5)(9)\cdot\frac(7)(2)=\frac(5\cdot7)(9\cdot2)=\frac(35)(18) Lai dalītu vienu kopējo daļskaitli ar citu, pirmā daļa jāreizina ar otrās apgriezto skaitli ( abpusēja ir daļskaitlis, kurā skaitītājs un saucējs ir apgriezti. \frac(5)(9):\frac(7)(2)=\frac(5)(9)\cdot\frac(2)(7)=\frac(5\cdot2)(9\cdot7)= \frac(10)(63) Ja viena no daļām ir naturāls skaitlis, tad iepriekš minētie reizināšanas un dalīšanas noteikumi paliek spēkā. Vienkārši paturiet prātā, ka vesels skaitlis ir tā pati daļa, kuras saucējs ir vienāds ar vienu. Piemēram: 3:\frac(3)(7)=\frac(3)(1):\frac(3)(7)=\frac(3)(1)\cdot\frac(7)(3) = \frac(3\cdot7)(1\cdot3)=\frac(7)(1)=7Pozitīvās un negatīvās frakcijas
Darbības ar daļskaitļiem
Frakciju samazināšana
![]() .
.
![]() .
.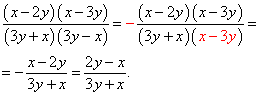
Daļskaitļu apvienošana kopsaucējā
![]() .
.![]() ,
,![]()
![]() ,
,![]() .
.![]() .
.![]() .
.![]() , un polinoms
, un polinoms ![]() , un polinoms
, un polinoms ![]() utt. Parasti viņi ņem tādu kopsaucēju, ka jebkurš cits kopsaucējs dalās ar izvēlēto bez atlikuma. Šādu saucēju sauc par mazāko kopsaucēju.
utt. Parasti viņi ņem tādu kopsaucēju, ka jebkurš cits kopsaucējs dalās ar izvēlēto bez atlikuma. Šādu saucēju sauc par mazāko kopsaucēju.![]() ;
;![]() .
.Daļskaitļu saskaitīšana un atņemšana
![]() .
.![]() .
.![]() .
.![]() .
.![]() .
.![]() .
.Daļas pamatīpašība
![]()
Daļskaitļu apvienošana kopsaucējā
Darbības ar daļskaitļiem
![]()
![]()
![]()
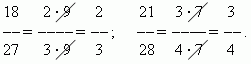

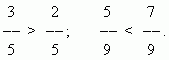
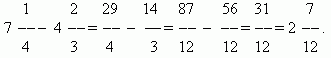
Frakciju samazināšana
Daļskaitļu apvienošana kopsaucējā
Frakciju salīdzinājums
Piemēram, \frac(9)(14) Daļskaitļu saskaitīšana un atņemšana
Jaukta skaitļa pārvēršana nepareizā daļskaitlī un otrādi
Decimāldaļas pārvēršana parastā daļskaitlī
Daļskaitļu reizināšana un dalīšana